Poison
Introduction
This page is all about the non-spell effects of poison. For the spell "poison", see Poison. It starts with general information and sources, and delves into mechanics and finally mathematics of Poison.
General Information
Poison in Eternal Lands is a condition where the player loses a constantly decreasing amount of health. A remedy for this condition is the potion Poison Antidote. Pre-Toadstool poison involved losing 1 health point per time interval for a maximum of 5-10 health points. Now, poison has a formula based on the time left. We'll get to the mathematics later in this guide. Some qualitative observations we can make in this section:
- Each poison lasts 3 minutes, and they are cumulative, meaning each additional poison adds another 3 minutes.
- Due to the nature of the cumulative formula, having only one dose of poison at a given time will yield the least damage.
- Three ways to tell poison has occurred, besides loss of health, are: (A) A green icon in the lower left of the screen, just above the mana display. (B) A green particle eye-candy visualization around the avatar. (C) A message in the console in red print.
The poison icon and particle visualization will continue until a green 0 is displayed for health loss. When the poison message is displayed, there is a 10 second delay before the first damage, and each additional damage is separated from the last by 10 second intervals. The 10 second delay means that the total time from the poison message display to green 0 display is 190 seconds, or 3 minutes 10 seconds.
Sources
- Using Toadstool, has a 1/21, or approximately 4.8%, chance of yielding a poison.
- Being attacked by a Red Snake or Skunk has a chance of yielding a poison, which is lessened by wearing armor.
- Using a Potion of Invisibility has a 30% chance of yielding a poison.
Mathematics
The formula entropy posted for poison damage was:
- P = 1 + (D-30)/30, where P = the damage from poison, taken every 10 seconds, and D is the duration left in seconds.
However, this produced results that were slightly off, so we have to take rounding(in this case, truncating) into account. The derived formula that will produce accurate results is:
- P = 1 + Truncate[(D-30)/30], where P = the damage from poison, taken every 10 seconds, and D is the duration left in seconds.
Truncate means that if [(D-30)/30] produces a fraction, always round down. By expanding the fraction, the 1s will cancel out, and we can simplify this, with a few exceptions.
- P = Truncate(D/30) works except for where D is between 0 and 30. Therefore, we must create a piecewise function to account for all scenarios.
The final formula is:
- P =
*Truncate(D/30) where D = 0 or D >= 30
*1 where 0 < D < 30
This means that the approximate(results will be thrown off by the truncation of decimals and when P = 1) duration can be estimated by multiplying the interval damage (P) by 30. This can be extremely useful.
- D = 30P
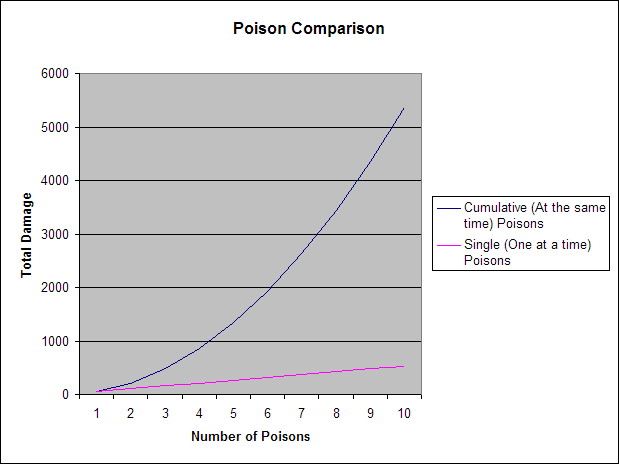
Another useful formula will be total damage yielded from a certain amount of simultaneous poisons.
- (File:Summation.gif + 2) gives the total damage of P poisons
The graph of this looks like this:
The main observation we can make from this is that it is beneficial to have as few poisons as possible at any given time.
Table
This table of values is to help estimate damage remaining for a poison interval. IE, if a 5 was the last damage taken, look across from 5 on the table for total damage remaining. Since the formula is based on truncating a fraction with 30 as a denominator, each amount of damage will repeat for 3 hits, except for the initial amount, and the final amount of 1. Therefore we will assume the damage is the first one of that value. Also, the table gives damage counting the said hit. So, subtract 1, 2, or 3 intervals, depending on if it is the first, second, or third hit of that type, respectively.